MBD PID制御系設計研修
目次
Part1 MATLAB/Simulinkによるモデル構築
MBDプロセス研修のページをご確認ください。
Part2 物理モデリングの基礎
流出流量は液位に比例する…という部分をどう描けばいいかがちょっとまだわかっていない。物理的におかしなところはないか?(h=0なのに、qoutに値が入る構図)という点で見ればいいのか?その「アタリ」の付け方のコツを知りたいと思います。言われてみればわかる…という感じでした。
非常に重要かつ難しいご質問です。一つの見方として,ユーザが任意の時間で自由のその値を決定できる信号かどうか(すなわちいかなる状況においても独立に設定できる信号かどうか)という視点から考察されるとよいと思います。
また,Part2で説明するアナロジーによる物理現象の理解ができるようになると,類似する物理現象との対応関係から,システムの状態に異存する信号をより見つけやすくなると思います。
演習2-1(2)ですが比較演算してからh[m]>=H[m]になったときにquotをH[m]にするで合っていますでしょうか?しかし、比較演算はまだ出てきていない?
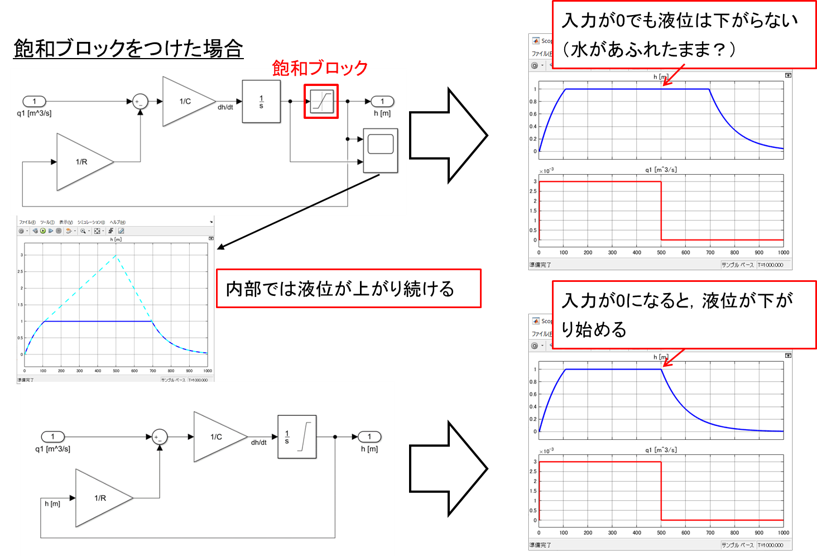
上記の比較演算は飽和(Saturation)ブロックを用いることで実現できますが,実際には解答にあるように積分ブロックの設定によって実現しなければなりません。以下に飽和ブロックを用いた場合と積分ブロックの飽和機能を利用した場合の結果の差を示しますのでご参考にしてください。
Q H(タンク高さ)をパラメータとして設定していますが、モデルには含まれていません。何のための定義になりますか?
こちらのパラメータは演習課題2-1(2)のために利用します。
演習問題2-1(2)について、水位があふれる液位なったときに頭打ちでh[m]の最大値を H[m]というシステムを作成しようとしているが、.mファイルのほうでhの最大値をHに設定すればよろしいでしょうか。
はい,Hも直径などと同様にタンク固有のパラメータの一種ですので,mファイル上で管理をすることをお勧めします。
タンクの液位のモデルで出てきたシステムパラメータですが、例題としてはすでにR=500[s/m^2]などのように与えられていましたが、実際の問題ではRの値が不明なケースが多いと思います。そのような場合、どのようにRの値を決めるのでしょうか?
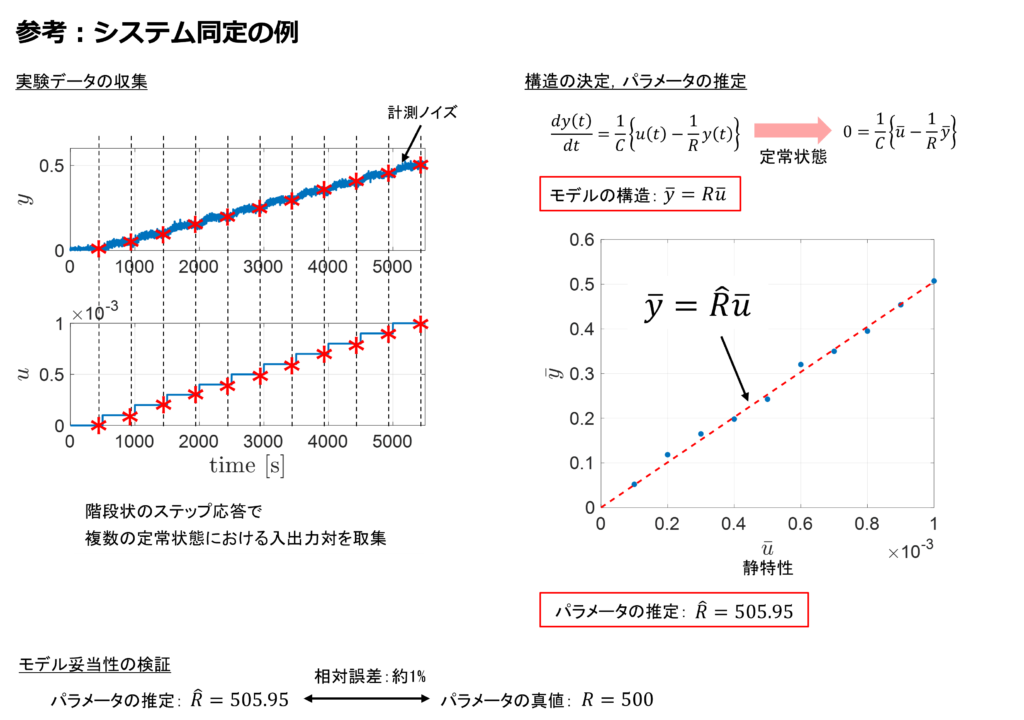
ご指摘の通り,モデルのパラメータにおいて,タンクの直径や高さなど直接計測できるパラメータがある一方で,出口抵抗のように直接計測できないようなパラメータも多く存在します.このようなパラメータを推定する方法(数式モデルを作成する方法)の一つとして,
「システム同定」があげられます.
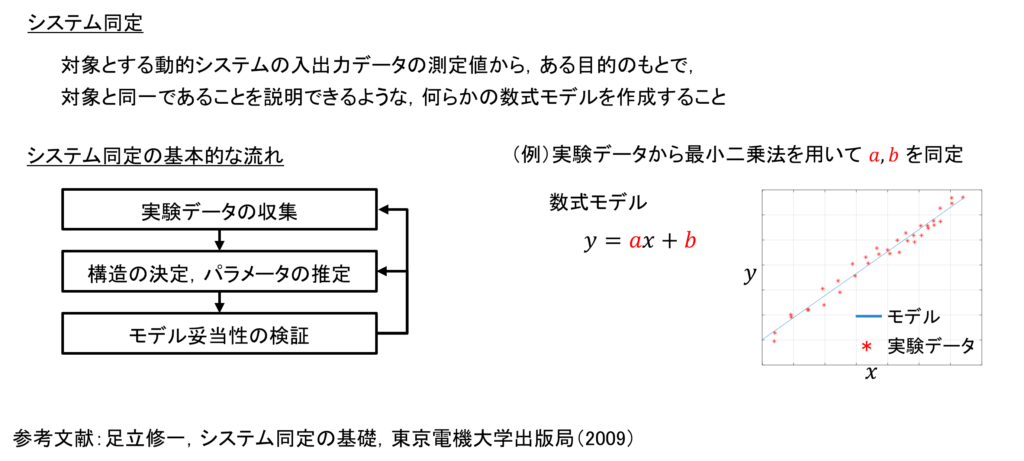
Matlab Simlinkのモデルを使ってパラメータスタディを行う際に、複数の条件を一度に回す方法(バッチラン)はありますか?
例えば,関数parsimを用いることで,一つのSimulinkモデルに対して,異なる条件のシミュレーションを一度に実行することができます.
また,Parallel Computing Toolbox (有料)を用いることで,シミュレーションを並列に計算させること(シミュレーション時間の短縮)ができるようです.
参考:
複数のシミュレーションの実行
https://jp.mathworks.com/help/Simulink/ug/introduction_bvnw33f.html
関数parsim
https://jp.mathworks.com/help/simulink/slref/parsim.html
詳細については,MathWorks社のサポートまでお問い合わせいただけますと幸いです.
Part3 システムモデルと伝達関数
原始関数の導出やラプラス変換がまだ、完全には理解できない。現状、感覚的に理解にとどまっている。色々なモデリングを模写として理解を深めていく。他にいい理解方法などはなるのでしょうか?
おっしゃるように,様々なモデリングを行うことで基本的なモデル化のパターンをつかんでいただくことがよろしいかと思います。
モデリングの際には,下記の原則を意識することで物理的に正確なモデル化が可能になるかと思います。
・ 足し算・引き算において各項の物理単位がそろっているか?(異なる物理量の加減算はできないため)
・ 保存則が成り立っているか?(若干経験が必要,基本的にはPart2 2-25の1.の考え方を用いる)
・ 係数を掛け算する際に変換後信号=係数×信号において変換後信号の単位が所望の単位に変換されているか?
ラプラス変換のやりかたは表をみながらならできるようにはなったが、前提があるからこそ導くことができたが、実際の現場では決めることができない場合はどうすればいいんでしょうか?
車両の挙動は、外乱によって動作は保証できないため、どこまでを閾値とすべきなのか?経験則になるのでしょうか?
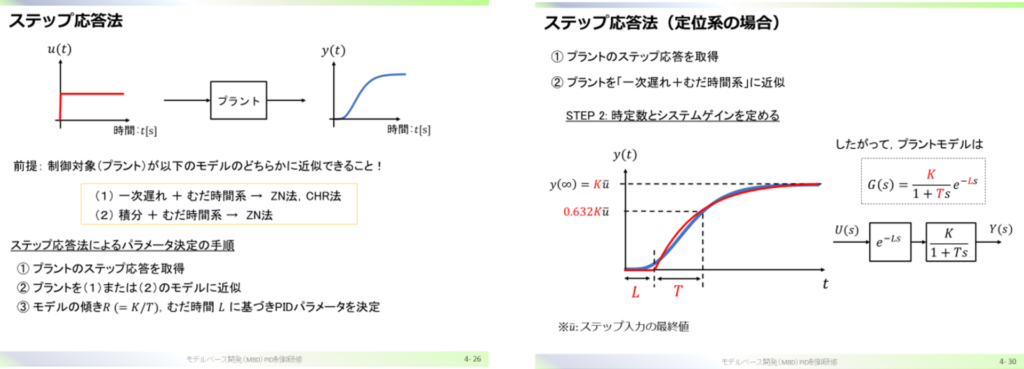
微分方程式からもモデリングが難しい場合,システムのステップ応答試験の結果などを用いて仮のモデルを作成することがあります(これをシステム同定と呼びます)。例えば,Part4のp4-26で実施したZN法(ステップ応答法)やCHR法において対象システムの応答から一次遅れ+むだ時間系のパラメータT,K,Lを推定しましたが,これが最も簡単なシステム同定の方法になります(作図法といいます)。パラメータ同定の方法にはさまざまな種類があり,構造とパラメータを同時に決定するような方法も提案されています。
また,モデル化誤差や外乱の影響を考慮し安定動作を理論的に保証する設計手法をロバスト制御系設計と呼びますが,本研修ではその詳細については割愛をさせていただきます。
昔、業務で振動解析などを行っていました。
ラプラス変換することによって、周波数領域でシステムを見ることができるようになるのではないかと思いますが、システムの周波数特性を見たい場合などは具体的にどのような操作があるのでしょうか?

Tank2の伝達関数の計算について省略されましたが、詳細について教えていただけませんか。

複数のシステムが結合したシステムでも、それぞれの伝達関数の組み合わせで表現でき、設計上の見通しは良い。実際の製品において、どこまでの規模まで適用するのが適当なのか、考え方があるのか気になった。
伝達関数の活用の規模についてはケースバイケースですので統一したお答えが難しいところです。化学反応プロセスの場合,化学反応を含む入出力関係(原料の投入量に対する温度の変化など)を「一次遅れ+むだ時間系」と多く繰りで表現することもあれば,機械システムの場合はモータや油圧シリンダなど,コンポーネントレベルで伝達関数を規定して結合するケースもあります。
制御対象の入出力関係を伝達関数で表現した方が見やすいとのことでしたが、
逆に伝達関数表現より状態空間モデルの方が適している場合があれば教えて頂きたいです。
状態空間モデルでは,変数の初期値を陽に取り扱うことができます。そのため,伝達関数のようにシステムの出力の初期値が0であるという仮定が不要です。また,多入力・他出力系に対する制御器設計を行う場合,状態空間表現の方が適している場合があります。
その他,現代制御系設計(LQR),カルマンフィルタなど,状態空間モデルをベースとした理論を適用する場合には状態空間表現が必要になります。
不完全微分についてもう少し詳しく教えて下さい
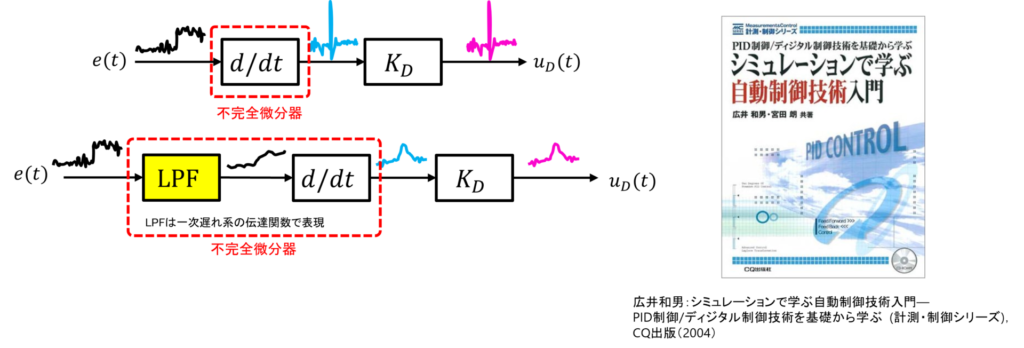
Part4でも説明をしておりますが,PID制御器をそのまま実装すると,目標値がステップ状に変化や計測ノイズに含まれる高周波成分が微分動作によって増幅され,入力が振動的になる(あるいはスパイク状の入力が発生する)という問題が生じます。
下図にあるように,微分器の前段にローパスフィルタ(LPF)を挿入することで微分器への入力信号に含まれる高周波成分をカットしでその動作を安定させたものを不完全微分器と呼びます(微分動作の高周波特性が純粋な微分特性にならないという意味で不完全という言葉が使われています。このことについて,参考書籍著者の広井氏はそのネーミングに苦言を呈しています)。詳しくは各種書籍や下記の参考URLをご参考にしていただきたく思います。
参考:
PID制御のお話
https://www.m-system.co.jp/mstoday1/MSTback/data/2004/11/PID_T.html
とりあえずフィードバック制御
https://hi-ctrl.hatenablog.com/entry/2018/02/25/020939
冒頭で動的モデルと静的モデルの解説があり、線形システムと非線形システムについて、少しだけ触れていました。
非線形なシステムの具体的な例を教えていただけますか?
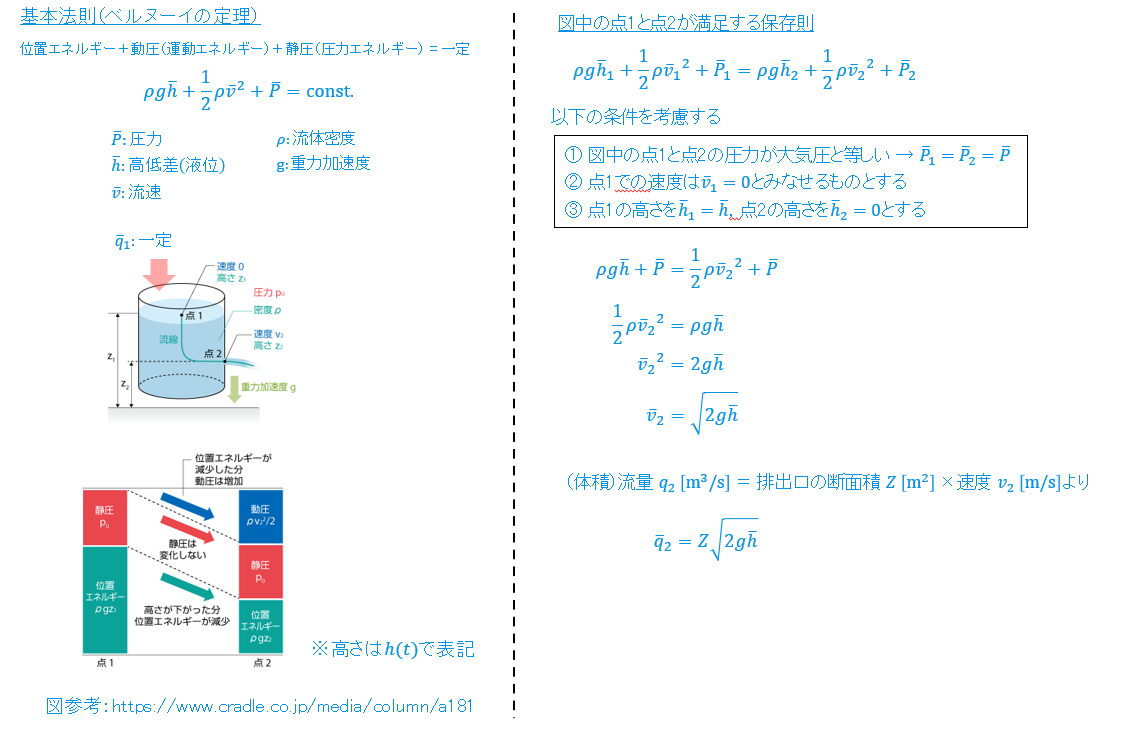
例えば,タンクシステムに場合は,ベルヌーイの定理により非線形な微分方程式を得ることができます(導出は下記参照)。
なお,タンクシステムの非線形性を考慮したモデリングについては拙著 山本編:「改訂 実習で学ぶモデルベース開発」にて解説をしておりますのでそちらもご参照いただけますと幸いです。
参考:ベルヌーイの定理に基づくタンクモデルの導出
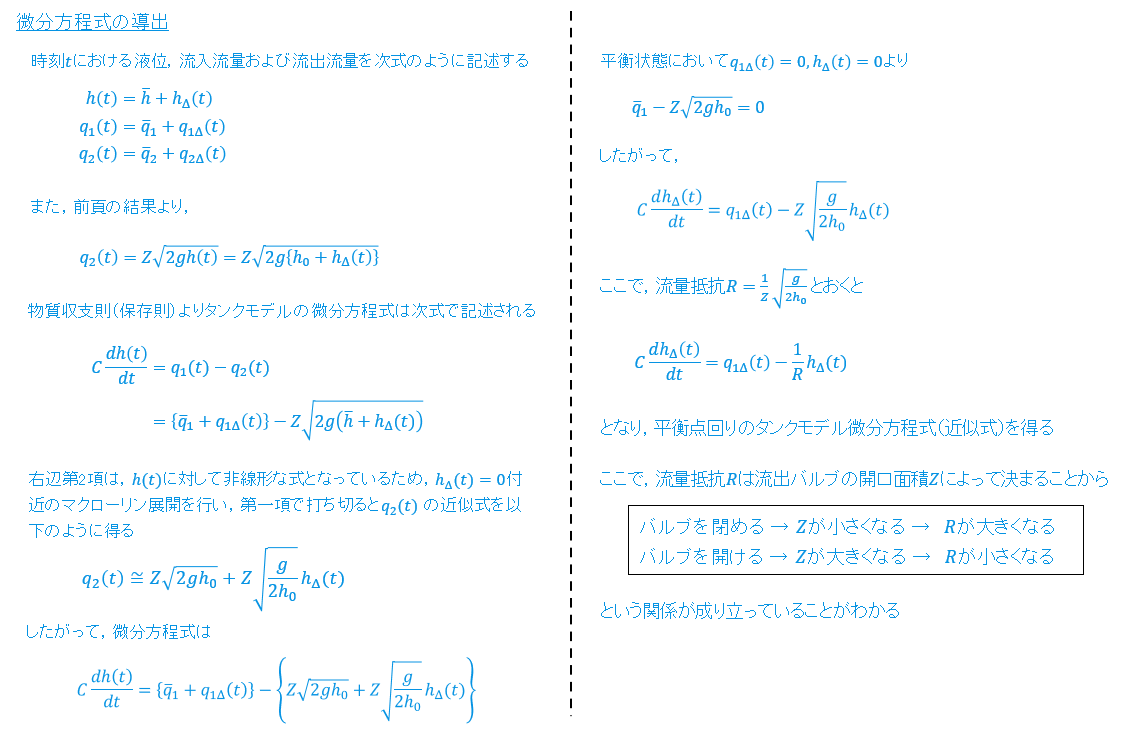
Part4 PID制御の基礎
コントローラーにKはalpha/Dになるのはなぜでしょうか。

FF,FB制御の理解を深めることができた。開発しているうえで、FF+FBを見たことがあるが、位相遅れはFFで改善することができるものでしょうか?
おっしゃるように,FFにより位相遅れが改善され高速な応答を実現することが可能になります。
人間が行う制御は行動内容によってコントローラの手法や数が異なるような気がしました。
実際の制御設計では、制御したい出力が複数ある場合、出力の数だけ個別にコントローラを作成するものなのでしょうか。
人間自体がどのような制御を行っているというかを正確に把握するかはなかなか難しいのですが,人間の行動を模した制御系設計(例えば,フィードバック誤差学習)などが提案されています。
また,入力と出力が複数ある系を多変数(MIMO: Multi Input – Multi Output)系と呼びますが,対象の制御を一つのコントローラで行うことも行います。この分野の研究は多岐にわたりますので,ここでは詳述を控えますが,例えば現代制御系設計における状態フィードバック制御器がこれにあたります。
前の動画で、プラントの特性をソフトでカバーし、機能目標を満たすのが制御、というような内容がありました。現段階では目標値追従を機能目標としているかと思うのですが、制御設計の現場で考える機能目標は他にもあれば教えて頂きたいです。
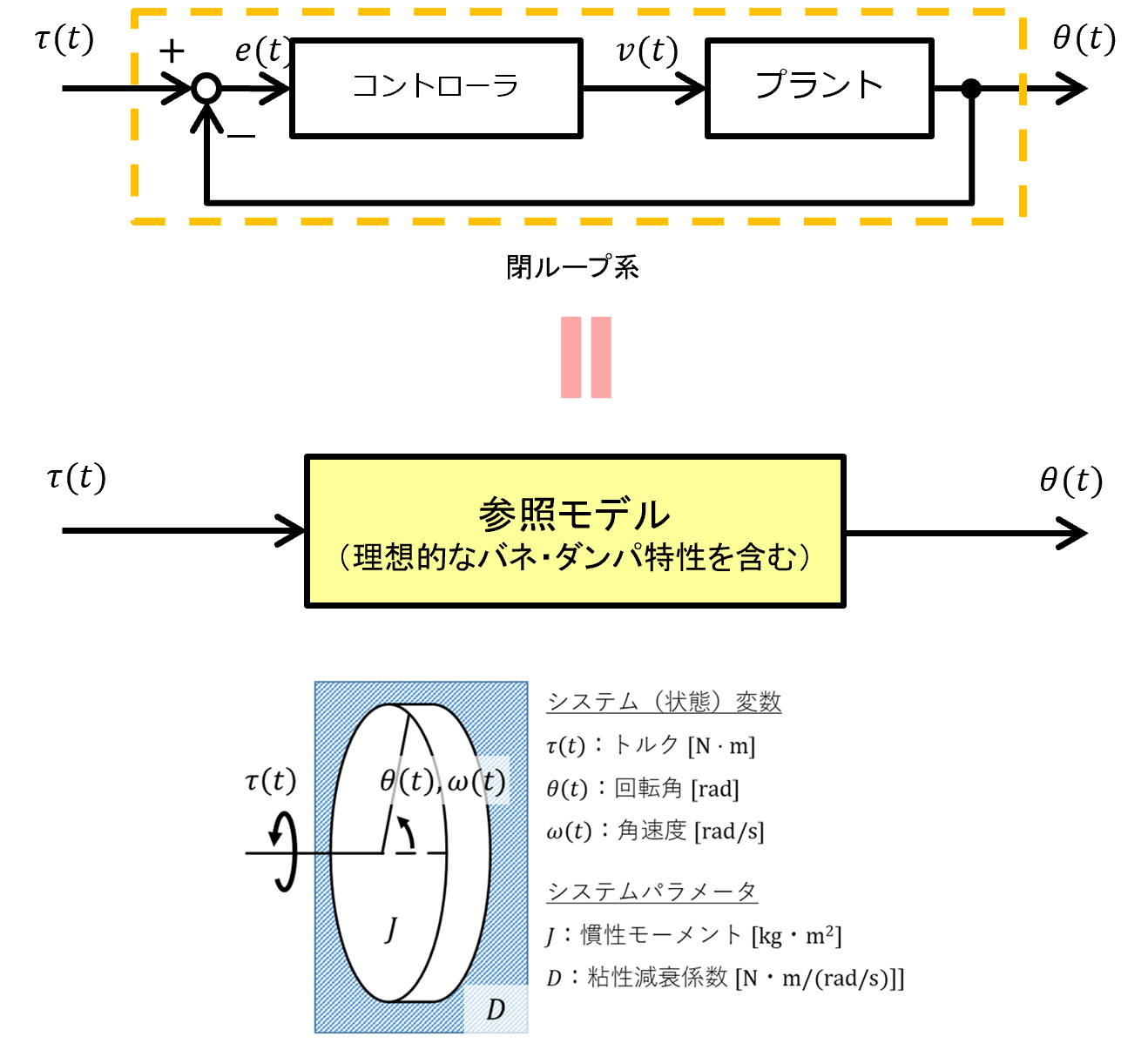
例えば,プラントにモータを用いて以下のような構成を考えます。この時,閉ループ系が外部からの入力に対して理想的な回転運動特性を持つ(具体的には,ばね定数や粘性減衰係数が所望の値になる)ように参照モデルやコントローラを設計することをインピーダンス制御(または,ばね定数だけを調整する場合はコンプライアンス制御)といいます。
実際に業務の中でPID制御器を使っておりましたが、Dの部分は0(実質使っていない)だったのですが、その理由の理解が進みました。
一度目標値を超えて目標値に収束するケースがパラメータを振ることで確認できましたが、目標値を超えずに収束させることが理想の設計なのでしょうか。
理想の応答は制御適用先の機器や仕様要件によって異なります。なぜそのような応答にする必要があるのか(Part5の例であれば,なぜその立ち上がり時間を設定する必要があるのか)という,制御系の応答の先にある要求を明確化しておくことが重要です。
例:温度制御システムの場合
例えば,温度制御システム(アクチュエータはヒータのみ)の昇温制御を考える場合,システム自身に冷却要素を持たないため,オーバーシュートが起こると,自然放熱による冷却を待たなくてはなりません。システムの熱容量が大きい場合や外気との熱抵抗が大きい場合,放熱には時間がかかるためオーバーシュート後の目標値復帰に時間がかかることになります。そのため,熱システムの多くは上記理由などによる生産性の低下を防ぐため,オーバーシュートが起こらずかつ速やかに目標値追従が行われる制御パラメータ調整を求められることなどがあります。
D制御は応答遅れを持つシステムに有効ということですが、むだ時間を持つシステムについても、同様に有効に働くのでしょうか?
D制御によってむだ時間を有するシステムの制御性能を改善できる可能性はありますが,むだ時間の影響を完全に取り除くことはできません。厳密には,むだ時間は出力フィードバックでは補償できない(どんなフィードバック制御器を設計しても閉ループ系のむだ時間がプラントの持つむだ時間より短くなることはありません)要素ですので,D動作によってむだ時間による位相遅れの影響を緩和する(たとえば,過渡応答時に生じる振動抑制など)程度にしか働かないと思っていただければと思います。
また,上述のようにD動作が位相遅れの影響を抑制できるか否かの指標として,産業現場では時定数とむだ時間の比率(L/T:L バイ T)指標というものが用いられることがあります。このL/Tが0.1を超えると(すなわち,時定数に対してむだ時間の割合が10%を超える)とPID制御によって良好な制御性能を得ることが難しくなることが知られています。
なお,むだ時間補償機能を有する制御構造には,
① スミス補償器(あるいは内部モデル制御器): 西脇ほか:制御理論講和(その3)ー むだ時間 ー,津山高専研究紀要(2002)
② スミス補償型PID制御:西崎 晶: スミス補償型I-PD設計法の研究,法政大学(1995)
③ 通信外乱オブザーバー: 名取ほか:通信外乱オブザーバを用いたむだ時間補償法,自動制御連合講演会講演論文集(2007)
などがあります。
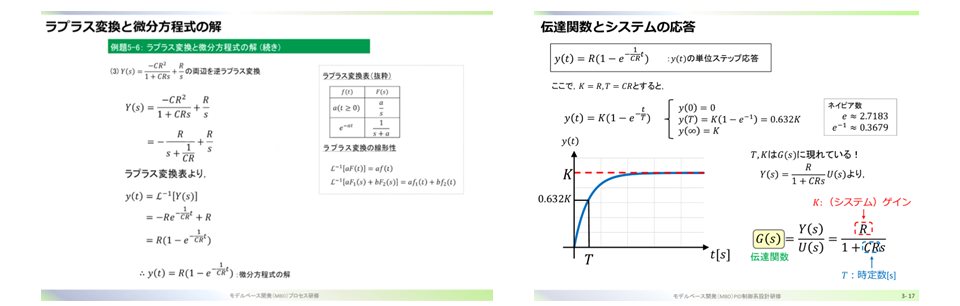
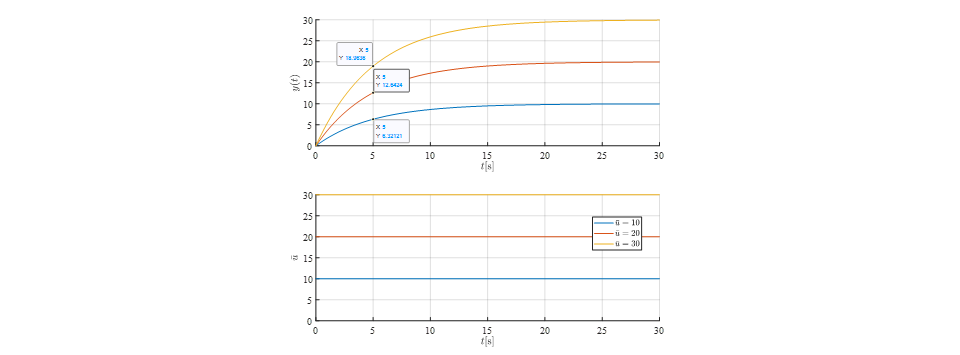
ステップ応答法の遅れ時間0.632Kuとは何処から算出されたものなのでしょうか?

微分制御則にて、一般的にフィルタとセットで使われることが多いとのことですが、具体的にどんなフィルタ(ハイパスとかバンドパスとか)がよくつかわれますか。システムの特性で別れると思いますが。
微分動作に対するフィルタはシステムの特性にかかわらず,通常,ローパスフィルタ(一般的には一次遅れフィルタ)を用います。
これは,微分による雑音成分(すなわち高周波成分)の増幅を抑える目的で利用されます。

無定位系のステップ応答を求める際、R={y(t)-y(t-Δt)} / (~uΔt) をラプラス変換する際の変換式が不明でした。

フィードバック制御器が複数連動する(ある制御系の出力を基に別の制御系の入力が決まる場合)システムは経験上収束しにくい問題があると考えています。
これを解決するためには、制御パラメータの調整より、制御器を最小限に簡易化する、あるいは制御対象を絞り込む対策の方が根本的な解決手法となるでしょうか。制御が思い通りにならない場合の分析方法(目の付け所)が分かると、実務でも応用できると感じました。
実応用上,非常に重要なご指摘をいただきありがとうございます。確かに,おっしゃるようにあるループの制御入力(または出力)がほかの系の入出力関係に影響を及ぼす形を干渉系と呼びます。
この干渉系の制御にあたり,非干渉化補償器を導入するケースがあります。非干渉化補償器を適切に設計することによりループ間干渉の影響が抑制され,多重ループ系の調整が単一のフィードバックループと同じように実現できます(下図参照)。
また,プロセス制御などではどの入力でどの制御変数を制御するか(ペアリングと呼びます,下記書籍参照)の指標なども提案されています。これにより,あるループが別のループに及ぼす干渉が最も少なくなるような制御系を構成することができます。
ただ,上記については画一的な設計論は存在ませんので,高い専門性とシステムへの理解が不可欠かと思います。ただ,制御器の構成を最小化する(特にPID制御ではなくPI制御で制御を行うなど)というスタンスは,設計上きわめて重要です。

PIDパラメータの調整方法について理論上は理解できたのですが、実際のプラントなどでどの様に求めているのかもう少し具体的に知りたいです。
例えば,汎用のデジタル調節計(下図)などにおいてはオートチューニング機能などが内蔵されており,対象のシステムに対して以下の手順を自動で行います。
① ステップ信号やリミットサイクル信号などの信号をシステムに印加し,システムの応答からシステムパラメータを推定(システム同定)
② 同定結果に基づきPIDパラメータを調整する
本研修内容を含めモデルベースドなPID調整アルゴリズムにおいては,①で得られるシステムモデルの精度が制御結果の良否に影響を及ぼすためその同定が重要になりますが,参考URLでも説明があるように,システム出力をわざと変化させるように入力を印可するため,システムへの負担が大きくなります。近年では,制御運転中のデータを用いて①のプロセスを経ずに②のPIDパラメータを直接決定するデータ駆動型(またはデータ指向型)制御に関する研究も進んでいます。

ステップ応答法はオイラー法と似た考え方なんでしょうか?
ステップ応答とオイラー法はその目的や手法が異なります。
ステップ応答法はシステムの特性を知るためにステップ信号を印加し,その出力結果からシステムモデルを構築しパラメータを決定する方法です。(例:ステップ応答のデータからシステムを一次遅れ系に近似し,そのパラメータのT,Kをデータにフィットするように求めた)
一方,オイラー法は微分方程式の数値解法になります。(例:微分方程式で与えられたモデルの挙動をオイラー法に基づくプログラムを用いて,計算しその出力結果を表示した。)
Part5 参照モデルに基づくPID制御器設計
モデルマッチングにおける参照モデルを二項係数モデルとするところが理解できなかった。
参照モデルの形式は二項係数モデルに限る必要はありません。今回は,システムの立ち上がり性能のみを考慮した参照モデルとして二項係数モデルをご紹介しました。
Part7では,二項係数モデル以外の参照モデルの設計法についてもご紹介いたします。
現場で好まれる制御は、人のチューニングしやすさが大きいように感じますが、大量生産するような製品開発では、どのようなポイントに注意して制御方式を決めるのでしょうか。

今回は2項係数モデルを参照モデルとしていたのですが、ほかにも参照モデルは提案されているのでしょうか?
はい,Part7では,二項係数モデル以外の参照モデルの設計法についてもご紹介いたします。
Gm_D=cell2mat(Gm, Denominator)において、’Denominator’が未定義です。というエラーメッセージが表示される。
cell2matのGmとDenominatorの間は「,(カンマ)」ではなく「.(ドット)」になります。資料が見づらく申し訳ございません。
Gm_D=cell2mat(Gm.Denominator)
tf関数の定義が気になりました。
tf関数の基本的な使い方は
tf([分子多項式のパラメータ係数ベクトル], [分母多項式のパラメータ係数ベクトル])
になります。
それ以外にもオプションの設定などがありますが詳しくはMathworksのホームページをご参照ください。
PID、PI-D、I-PDと制御器の構造が変わると制御性が変わるということを理解した。新しいシステムの制御を考えた時、制御構造をどのように検討するのかが気になった。
制御器を検討される際には,制御応答と制御入力の双方で比較をされるとよいと思います。特にスパイク状の制御入力が発生するとアクチュエータの故障の原因となるため,微分フィルタの利用やPI-DやI-PDの使用が望ましいと思います。
キックについてもっと詳しい説明を頂きませんでしょうか(定義など)?
動画の最後のI-PD制御器部分で、参照モデル立ち上がり時間sigmaの値を0.5から0.25や0.1に変換すると、比例動作によるキックはまた出てくるみたいです。
ここの結果とPI-D制御器の結果との違いは、少し上昇時間がありそうです。これはキックと言えますか?
一般的には,キック現象は「微分キック」を指すことが多く,「目標値(あるいは制御偏差)の急峻な変動に伴って操作量が微分動作のために急峻に変化する現象」で,操作量が「0 → ピーク値」に一瞬で変化する現象とご理解いただければと思います。動画でもありましたように,比例キックをいう表現を用いる文献はあまり多くありませんが,操作量の急峻な変動を起こすという意味で,今回は比例動作によるキックという表現を用いています。

PID、PI-D、I-PD制御の特徴を演習を通じて理解できました。
I-PD制御において、分子を合わせるような作業を行っていないにも関わらず参照モデルと出力が一致する理由が完全には理解できませんでした。
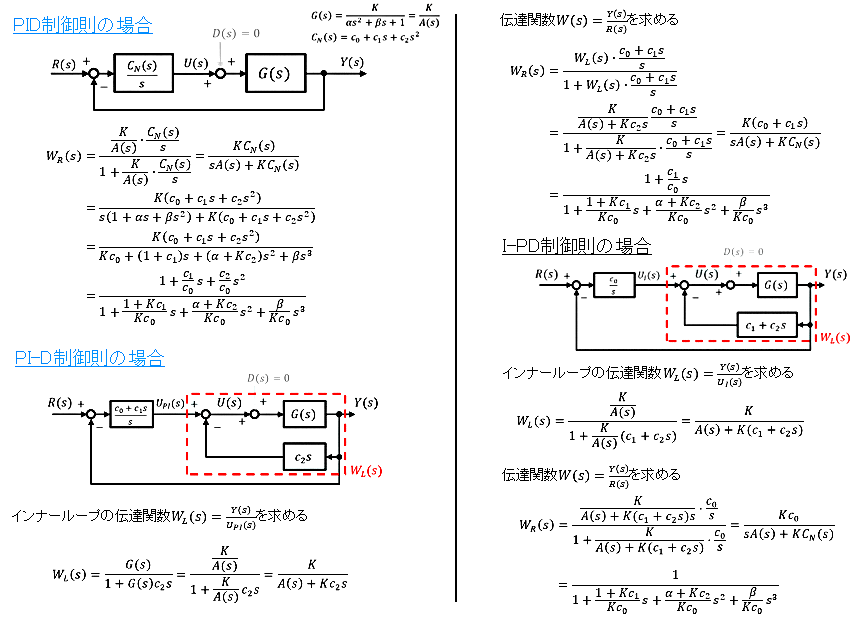
動画では説明しておりませんでしたが,補足として配布テキストp. 5-23に,PID, PI-D, I-PDの閉ループ伝達関数の導出方法を掲載しております(同じスライドにはなりますが,次頁に掲載しております)。ポイントとしては下記の赤枠に示している通り,制御器の構造に依存して分子に「s」の項が出現します。I-PD制御器の場合,赤枠に「s」が出現しないため,参照モデルの構造と一致することとなり,モデルマッチングを実現することができます(詳細な導出は下記を参照ください)。
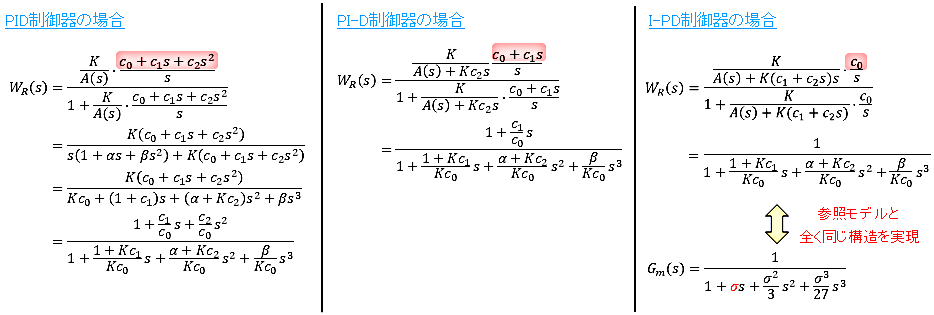
詳細な導出(補足:テキストp.5-23)
講義の中でどの制御を適用するかが大事と言われていましたが,実際にどの制御器を採用するのかは慣れでしょうか。
一般的にはI-PDよりもPI-DやPID制御器の方が応答は俊敏になります。その理由として,操作量の変動が大きいことは,誤差の修正能力が高いことを意味するためです。したがって,俊敏な応答が求められる場合は,PI-DやPID制御器を採用することも考えられます。しかしながら,事前にオーバーシュート量を正確に把握することが難しいため,ある程度,システムがオーバーシュートを許容できる場合でないと採用することは難しいと考えられます。
産業機械などでは、できるだけ高応答な制御が求められる場合があると思います。実際の適用においては、設計者がσ(立ち上がり時間)をシステムとして問題が出ないようにできるだけ小さく設定するということを試行錯誤的に行うのでしょうか?
σの設計指針については,実際の機器で調整することになると思います。特に制御対象にむだ時間が含まれる場合,高速な応答を求めすぎるとシステムが不安定化します。制御によってむだ時間の影響をなくすことはできないため,少なくともむだ時間よりも大きなσを設定する必要があります。
このような背景から,一つの目安として概ねの制御対象の時定数とむだ時間が分かっている場合,(時定数+むだ時間)の1/2~1/3程度で設定するケースが多いです。特に時定数とむだ時間の比 L/Tが大きければ大きいほどσは保守的(大きな値)にする必要が生じます。
目標値がステップやランプのように直線的でなく、変化するような場合も実際にはあるかと思いますが、その場合はどのような制御設計が必要になるのでしょうか。
制御機設計は様々なバリエーションがあるので,一概には言えませんが,PID制御器の場合でも変化する目標値を区分的にはステップ応答の大きさが連続的に変更されているとみなすことができる範囲では,有効に作用します。
そのほかにも,モデル予測制御(MPC: Model Predictive Control)や適応制御(Adaptive Control)などの制御系設計手法もありますが,これらの設計手法はやや煩雑になります。
ロボット開発企業のBoston Dynamicsが開発中の二足歩行ロボット「Atlas」の動画を見て感じたことです。人間のようにミス(バグ?)を含むプラント・コントローラを簡易的に再現できるようなモデル構築手法はあるでしょうか。製品が意図しない使われ方・動き方をした際の制御も含めた安全性の確保ができると設計者は安心して製品を世に出せると考えています。代表的な特性(ミスのパターン)をいくつか検証して制御器設計等をするのでしょうか。
自動車開発などでは,シミュレータに様々な「シナリオ」を設定し,その中で(主に)プラントや環境変化などをGUIなどを通じて設定できるソフトウェア等がございます。このシナリオのパターンをいかに設計するかが重要とは言われているものの,無数のシチュエーションが想定されるため,目的に応じて設計が必要かと思います。
参照モデルのイメージが自分の中ではしっくり来ていないが、入力に対する理想的な出力を簡易的に表したものだと理解しています。認識違いあれば指摘ください。
はい,ご理解の通りで結構かと思います。
出力信号を直接記述するのではなく,入力信号に対する「応答特性」としてモデルを用いて記述しているということになります。
産業機械などでは、台形な目標値を与える場合があると思います。台形な目標値の場合、立ち上がりの部分はランプ状の目標値と言うことができると思います。この場合において、PI制御はランプ状の部分は追従性が満足されないということができるのでしょうか?
はい,ランプ状の部分では目標値と出力に定常偏差が生じます。
極は分母多項式を特性方程式としたときの解で良いでしょうか?
ご質問通り,極は,特性方程式(分母多項式=0)の解になります。
今回の動画では触れておりませんでしたが,テキストp. 7-37にて改めて説明がありますので,ご参照ください。
一次遅れ系に対して極配置法に基づくPI制御を行うとき、立ち上がり時間σとシステムゲインK, 時定数Tがわかれば表よりKp, Kiが求められると理解しました。
あらためてKpを求める式を見ていたのですが、立ち上がり時間σが極端に長いとKpが負の値になる可能性があるかと思います。こういった、システムの時定数に対して参照モデルの立ち上がり時間が遅い場合はPI制御では対応できないということでしょうか。ご教示いただけましたら幸いです。
大変重要なご指摘ありがとうございます.結論から言えば,一次遅れ系に対するPI制御機の設計においてKpが負値を取る場合,PI制御器の構造や入力の制約の状況に応じて制御システムが破綻する可能性があります.
特に,PI制御構造をとる場合,極配置で設定したKpおよびKiによるパラメータの影響が,閉ループ系の分子多項式にも表れ,Kpが負値をとる場合,この影響がした図のように目標値印可後の逆応答として現れます.
なお,I-P制御の場合,原理的に閉ループ系に零点が生じないので,Kpが負でも所望の応答が実現できますが,産業機器(たとえばPLCや汎用温調器)によっては負のPIDパラメータを許容しないものもあるので注意が必要です.

Part6 実践!DCモータのPID制御
「二次遅れ系」=「PID制御」と直感的に判断できるものなのか?根拠を理解したいのですが、反復演習が必要だと感じました。

『モータの伝達係数を2次遅れ系から1次遅れ系に近似したい』理由が良く分かりませんでした。
一般的に制御系においては,同様の制御性能であればsの次数が小さい方が設計パラメータが少ないため設計の見通しが良く,モデル化誤差に対しても安定した性能が期待されます(モデル化誤差が大きいと制御性能は劣化します)。
本研修でもPID制御(次数は2) → PI制御(次数が1)とすることを考えます。実際,D動作はノイズを増幅する効果を有しているため,計測ノイズの影響で,入力の分散(バタつき)が大きくなる傾向にあります。そのため,PID制御においては次数を下げることによって,上記の問題を回避することが期待されます。
近似モデルを導出することができれば、少ないパラメータで設計できるようになることは理解できました。
一方で今回のようにインダクタンスLの1つ変数だけであれば、誤差がないように思いましたが、システムが複雑になれば近似する変数が増えていくでは?と思ったのですが誤差が増えていくのでしょうか。
おっしゃるように一般的には近似による誤差は複雑になればなるほど増加すると考えていただいて結構です。そのため,できるだけ近似誤差が小さくなるような要因を見つけることが重要になります。
ロータリーエンコーダーでSVの値を変更しても、値がうまく切り替わらなかったので、mファイルのSVの値を変更して確認しました。
(ロータリーエンコーダーが反応しなかったのは何か設定が悪かったのでしょうか?
「Rotary switch」と「Constant」ブロック(SV)のリンクが切れている可能性があります。
再リンク等の利用方法については下記のページをご参照ください。
PID制御を速度型+積分飽和に変更したことによって、uが微妙に振動するようになったように見えます。これは微分操作によるノイズの影響でしょうか?
おっしゃる通りです。具体的にはA/D変換器によって発生する量子化誤差が信号のノイズとなり,これが増幅されるために発生します。
ワインドアップ現象でお聞きしたいです。手動操作から自動操作に切り替える場合、PID演算を止めて積分を0にする事で対策になるでしょうか。
原理的には可能ですが,前回の入力値との連続性が担保されないため切り替えた瞬間に入力が急峻に変化する恐れがあります。
ワインドアップ現象の対策を速度型にすることで良くなるように思いましたが、微分ゲインを上げてしまうと逆に悪影響を及ぼすとの理解でよろしいでしょうか。
位置型・速度型にかかわらず一般的に微分ゲインは高周波を増大させるため,高周波成分を含むノイズ環境下では入力の分散が大きくなるという影響が懸念されます。
A/D変換器の取り込んだ値を微分演算を行う時にA/D変換器でサンプリングした値を微分しようとした場合、微分する値を取り込む時間はどの様に考えればよろしいでしょうか。例えば入力信号0~24Vを0~256ビットに変換するA/D変換器で1秒間あたり1V変化した場合、1秒間では10ビット変化していますが0.1秒では1ビット変化になります。0.05秒では整数で求めると0ビット変化になります。1Vの変化量を計算してそのレベルですので0.1Vの変化量ではもっとビットの変化量が少なくなると思います。A/D変換器の分解能を例えば8192ビットにすれば良くはなると思いますが、それでも小さい変化量は取れないように様に思います。また1秒での変化量で計算しましたが微分なのでもっと短い時間での変化量を計算した方が良いと思うのですが、微分する数値を取り込む時間に関してどの様に考えれば良いか教えていただけますでしょうか。
おっしゃるように実際のA/D変換器には回路上のA/D変換に必要な変換時間が生じます。ただし,これらの変換時間一般的には数ns~数μsで完了することが多く,msオーダ以上のサンプル周期をもつコントローラなどでは無視しても差し支えありません。また,コントローラの数値微分は一般的に,数値微分(現在のサンプル値と1ステップ前のサンプル値の差をコントローラのサンプル周期で割ったもの)を用います。
速度型にする際に、PIDのD項は二回微分となり、高周波成分の影響を受けやすくなる、とのご説明がありましたが、P項にも一回微分が入った為、こちらも高周波の影響を受けやすくなるのではないでしょうか。
前のご質問回答にもありますが,実際にA/D変換器の量子化誤差の影響(ノイズ)を増幅しています。
PID制御設計を行う中で、ワインドアップ現象が出た際に、どう対処するのかは理解出来た。事前に対処する方法はありますか?
今回ご紹介した速度型PID制御器は操作量が操作量飽和の範囲内で動作するのであれば理論的には位置型制御系と同じ制御性能となります。そのため,一般的には速度型PID制御器を採用しておくことで,予期せぬワインドアップ動作による不慮の誤動作を未然に防ぐことができると考えております。ただし,飽和領域での制御性能は担保できないため事前に予見できる場合には操作量飽和が起こらないように設計を変更する(例えば定格出力の大きなアクチュエータを選別し,操作量飽和にかからなくするなど)等の対策は考えられます。
サンプル時間を-1にするのはどういった意図があるのでしょうか?
サンプル時間「-1」は継承と呼ばれる設定です。今回の場合は,ソルバーで設定したサンプル時間の値が反映されます。ただし,サンプル時間の継承自体は複雑なモデルであるほどその動作が複雑になるので注意が必要です。詳細は,下記ページの「継承サンプル時間」をご覧ください。
HILSの計算は現実時間とリンクして計算しているという認識であっているでしょうか。
そうであれば、Simlink上で行っていたEndtimeよりはるかに速い計算とは、どのような違いがあるのでしょうか。
計算方式がMILSとHILSで全く同じ場合,計算結果に関してはそれぞれのシミュレーションで変わりません。
したがって,計算がサンプル時間内に完了するという理想条件においては,各ステップにおける計算出力のタイミングのみが異なることになります。
制御系を設計するにあたって、人命に係るような重大な機能に関しては複数制御系統を設けるのでしょうか。
例として、PID制御器が故障したと自己判断し、異常発生時の制御信号を別系統でプラント側に送る等の多重構造の設計手法は確立されていますか。
フィードバック制御器はパラメータの調整によって安定性が崩れるリスクを含みます。そのため,実用上はフィードバック単体では動かさず,ループの外側で,ご質問のようなケースでは,その制御性能を監視し万が一の場合の処理(フェールセーフ)を行う機構が必須です。
HIL演習にて、「実装してみるとノイズの影響からsigma=0.5が~」というお話がありました。実際、制御器を実用する上で機器の構成要素以外のノイズ(設置場所自体のノイズなど)を考慮してHILシミュレーションを行なうことはあるのでしょうか?
はい,制御においてはノイズに対する操作量の感度が重要です(操作量の振れが制御量の振れに直結するため)。したがって,ノイズの大きさに対する考慮も行うことが望ましいと思います。
今回MATLABで演習を行っていますが、Pythonでもされていますか。書籍でPythonによる制御工学入門などがあり、pythonでも出来たら面白いかと思いました。
Pythonでも制御工学のプログラミングは可能です。ただし,PythonにはSimulinkのようなブロックプログラミングの機能がありませんので,プラントモデルの表現等を全てコードとして記述する必要があります(Part1 p.1-14のMATLABによる制御系設計とほぼ同じコードになります)。

MILSの実験動画においてPID⇒I-PDの変更でワインドアップ現象がなくなったのを確認しましたが、
I-PDに変更することでワインドアップと微分キックを抑制できるという理解であっていますでしょうか。
位置型制御則=PID、速度型制御則=I-PDでしょうか。
PID・I-PD制御則,位置型・速度型制御則は下記の表のような分類になります。
速度型制御則: アンチワインドアップ
I-PD制御則: 微分キックの抑制

今回研修で使用したコントローラは,デジタルPID制御器には相当しないのでしょうか?デジタルPID制御器の実例をご教示頂けると幸いです。
実装の段階で実際にはデジタルPID制御器となっています。ただし,ソルバーの設定によって積分の演算が異なりますので,補足資料のデジタルPID制御器の動作と異なる可能性があります。
6-63「補足2:デジタルPID制御(PID制御器の離散化)」にて,離散時間位置型PID制御則から離散時間速度型PID制御則を考えるときに、赤字で「u(k)-u(k-1)を計算」とあります。位置型から速度型となると{u(k)-u(k-1)}/Tsを計算すると思っていたのですが,違うのでしょうか。

離散化した場合にシステムの処理時間の可能な範囲で極力サンプリング周期を小さくすれば連続時間系の応答に近づくと思ったのですが、小さくすることによってデメリットはあるでしょうか。
Simulinkを用いた微分方程式を含むシステムのシミュレーションでは数値積分(Simulinkではソルバーと呼ばれます)を用いた計算が行われます。おっしゃるように一般的には計算ステップサイズを小さくすることで,積分演算の精度は向上します。しかしながら,例えばオイラー法(ODE1ソルバー)などではステップ数の増加に伴う計算機の丸め誤差の累積や,同じ時間区間のシミュレーションであっても計算ステップサイズが小さくなると計算不可が増大するといったデメリットが存在します。そのため,プラントモデルにあった適切なソルバーを選択することが重要です。
プレフィルタの分子多項式の次数はどの様に決めるのでしょうか?プラントモデルの次数に合わせると考えて宜しいでしょうか?
一般的にプラントモデルの逆モデルは相対次数が0未満となります。そのため,プレフィルタの役割は分母多項式の次数を適切にとることでフィードフォワードコントローラのプロパー性を確保することになります。したがって,設計が煩雑になる場合はプレフィルタの分子は1としてもかまいません。
ただし,実際の制御においてより性能を求める場合などには,フィードフォワード制御器の相対次数を考慮しながら多項式として与えることも可能です。
・エクスターナルモードを選択できないのですが、どのようにしたら選択できるようになるか教えていただきたいです。
・実行モードの「エクスターナル」が見つかりませんでした。「ノーマル」「アクセラレータ」「ラピッドアクセラレータ」はあるのですが、「エクスターナル」がプルダウンに出てきませんでした。(バージョン:2021a) 一応「ノーマル」でも動きはしました。
・エクスターナルモードを選択できないのですが、どのようにしたら選択できるようになるか教えていただきたいです。
Simulink Support Packageが上手くインストールされていない,あるいは,バージョンによっては画面上にボタンが表示されていない可能性があります。
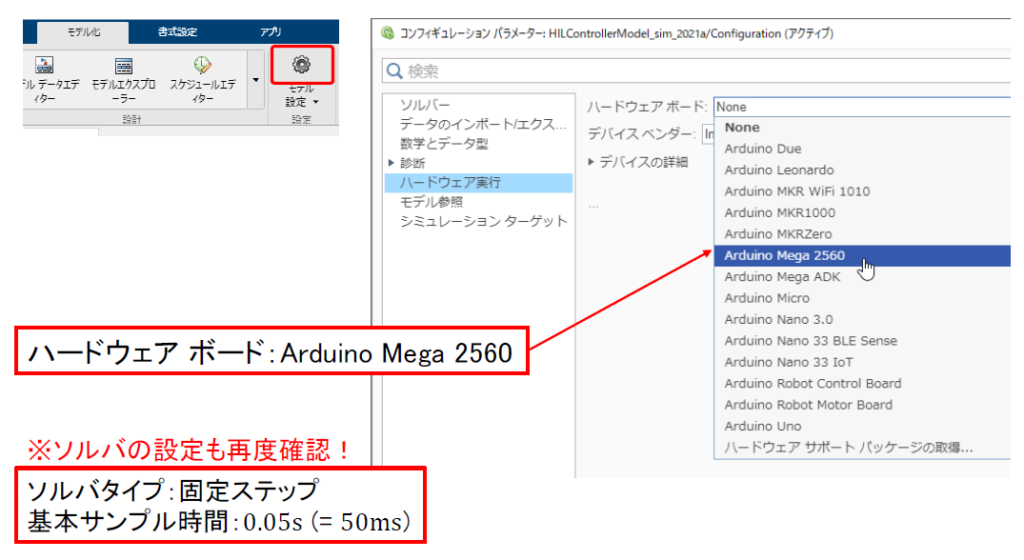
・ モデルコンフィギュレーションパラメータでハードウェアの選択が正しく行われているか確認してください。
・ 「ホーム」→「アドオン」→「アドオンの管理」からSupport Packageのインストール状況について確認ください。
・ 2019b以降のバージョンの方は、以下の操作をしていただくと、「ハードウエア」タブが表示され、「監視と調整」ボタンが出てきます。これが動画内でいう“エクスターナルモード”になります。
Part7 古典制御概論
講義資料はどこかで配信していただけますでしょうか?
産業応用事例等,一部の情報については配布資料に含まれておりませんのでご了承ください。
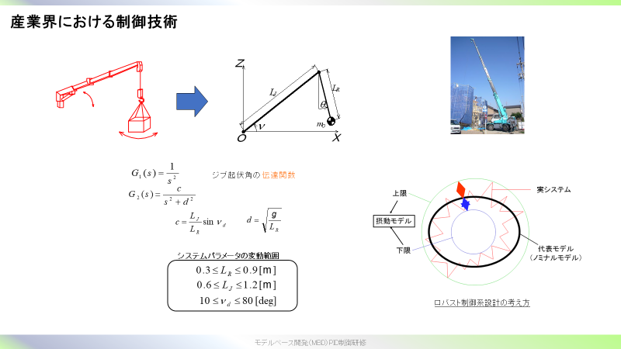
最初の方で説明のあったロバスト制御は安定性重視により制御性能はそこそこという印象を受けました。
データベース駆動型制御のように状況変化に対して瞬時に高性能な制御が可能な方が利用シーンは多いように感じますが、ロバスト制御ならではの良さはどのような点にあるのでしょうか。
ロバスト制御は,モデル化誤差やシステム変動による不確かさに対して,安定性重視の観点から制御系を設計します。システムがどのように変化しても,予め見積もった不確かさの範囲内であれば,制御系の安定性が確保されるよう制御系を設計します。
そのために,どうしても設計が保守的にならざるを得ません。したがって、「制御性能はそこそこ」と言われる通りです。 一方,不確かさを積極的に取り込んで制御系設計に活かす制御法に「適応学習制御系」があります。
紹介したデータベース駆動型制御法もその一つです。理想から言えば,この制御法の方が現実的のように思われますが,安定性が理論的に言えても,実装上で安定性が保証されるとは限りません。(※理論的な安定性は,様々な仮定(理想条件)の下で証明されていますので,実装の際にこれらの仮定が必ずしも満足されるとは限りません。)
この問題を何とか解決したいと,最近,データベース駆動型制御法を提案し,これに注力して研究を行っています。
以上のような理由で,産業界ではロバスト制御の方が安定性の意味で好まれているというのが現状です。
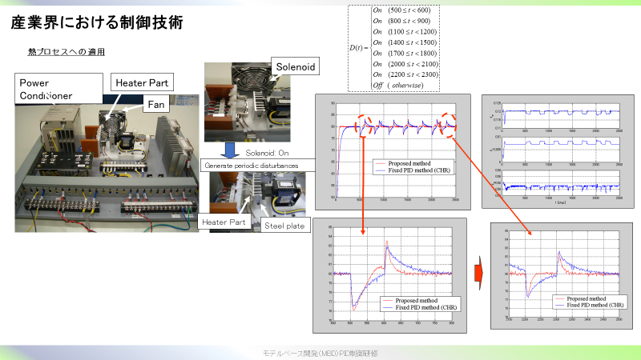
熱プロセスへの適用のページで、目標温度への収束を早めていた結果が示されていましたが、温度変化初期時の対応はあまり変化していないように見えました。これはデータベースに、温度変化初期時に温度変化を収束させるデータを与えてあげれば改善する見込みはある、という認識で良いでしょうか?
皆さんに紹介した「データベース駆動型制御」は,オンライン学習によるものです。ですので,初期の段階では,学習が進んでいないので制御性能は,それほど良いものではありません。学習が進んだ後には(最後の方では),望ましい制御性能が得られていることが確認できると思います。
オンライン学習は,産業現場では安全性の面からなかなか受け入れられません。このような現状から,研究室では,オフライン学習(あるいは,オンライン最適化)によるデータベース駆動型制御法についても開発しているところです。もしご興味がありましたらご連絡ください。
制御応答の早いシステムのケースで、シミュレーション上の理論値と実システムでの測定値が一致しているのか評価を行う場合、どの様な測定器を使用して評価されてますでしょうか。
測定装置については各社,業種別に様々な装置を利用されているかと思いますので一概にお答えするのが難しいところです。一般論として,モデルとの整合性を図るには,計測される信号の信頼性が重要になります。したがって広帯域(必要な応答を十分に取得できる応答性能)でかつ高分解能(量子化誤差の影響が小さい)で重畳するノイズの影響が少ない装置が必要となり,結果的に高額な計測装置を必要とするケースが多いかと思います。
MATLAB上ではSCOPEを使用していましたが、実システムでの測定器はどの様なものを使われていますでしょうか。
MATLAB上ではSCOPEを使用していましたが、実システムでの測定器はどの様なものを使われていますでしょうか。
コントローラ上の表示方法のみに限定させていただきますが,例えば,RCP(Rapid Control Prototyping)と呼ばれるMBDにおけるコントローラモデル検証用の専用ハードウェアを用いる場合,計測結果をプロットする機能がついているためこれらを用いるケースが多いと思います。なお,Speedgoat社のリアルタイムハードウェアはSimulinkモデルがそのまま実装可能であり,SimulinkのScope機能(Scopeブロックではなく,シミュレーション データ インスペクターと呼ばれる機能を用います)を用いてモニタリングすることが可能です。

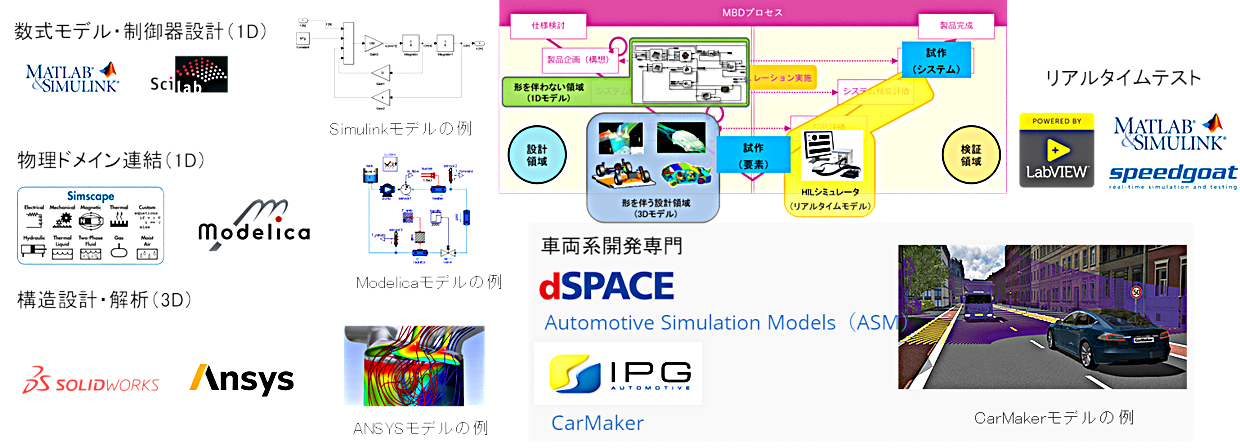
今回MATLABでの講義を行っていただきましたが、MATLABでのモデル構築をされる企業が多いでしょうか。
MBDのどの部分に注力をされるかによって必要なソフトウェアが異なります。MILS上流の1Dモデリング(特に制御器設計の場合)では,MATLAB/Simulinkなどが用いられることが多いですが,それ以外では専用の物理ドメインに対応したソフトウェアを利用する必要もあります。
詳しくは各種ソフトウェアベンダーへお問い合わせください。
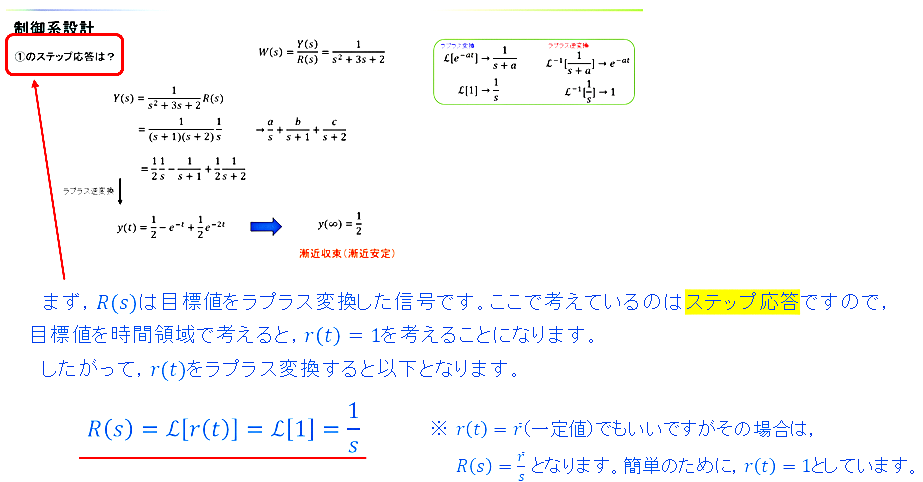
p.7-23の計算においてRが1/sとなるのはなぜですか?
モデルマッチング法は分子多項式の根が安定の時のみに適用できるとのことで実際に使うのはかなり限定的なのかなと思いました。
一方で、極配置法は分母多項式のみマッチングということでほとんどの場合に適用できるのでは?と思ったのですが、分子多項式がどんな形であっても適用できるのでしょうか。
言われている通りです。モデルマッチング制御法は,参照モデルに完全に一致する制御系を実現することから,対象とするシステムが最小位相系(分母多項式の零点がすべて安定な系)という条件が課せられます。一方,極配置法は分母多項式のみを一致させ,分子多項式は一切触りませんので,分子多項式がどのような形であっても構いません。ただし,分子多項式をフリーにしているために,厳密にはその影響が応答波形(特に過渡特性)に現れますので,この点にご注意ください。(その影響が顕著に出ない場合も多く存在します。)
ラウス配列表以外に安定性を判定する方法はあるのでしょうか?
特性方程式の係数を用いて安定判別する方法は,ほかにも代表的なものとして,ラウス・フルビッツの安定判別法などがあります。古典制御を対象とした著書(制御入門書)には,必ず紹介されているかと思いますので,詳細は著書をご参照ください。もし分からないようであればご連絡頂ければ,著書の紹介やこのことについて説明したいと思います。システムの特性方程式が与えられて,安定か不安定かを知るためだけであれば,Matlabのコマンドで特性根(極)が容易に算出できるので,わざわざ安定判別法を利用する必要もありません。制御系が安定となる制御パラメータ(例えば比例ゲイン)の範囲を算出したい場合などは,これらの方法を利用する意味があるかと思います。
上記以外にも,ナイキスト線図やボード線図を用いて安定判別したり,安定度(安定余裕)を見積もったりする方法もあります。これらの方法も,前述の著書では必ず紹介されていると思います。Matlabがあればこういった図を作図することも簡単です。

