MBD現代制御システム設計研修‐理論編‐
目次
Chapter01_現代制御概論
最適設計(過渡応答最低化/エネルギー最小化)の話は、後半で出てくるのでしょうか?
(目次になかったため)
最適設計につきましては,6.3節(P.88)でご説明させて頂いております.
Chapter02_数学的準備
ヤコビ行列にする目的を教えてください。
今回の講義では,第3節で,近似線形システムの係数行列を算出する際にヤコビ行列を用いております.なお,ヤコビ行列は,「関数の傾き」に対応しております.
ヤコビ行列はどんな時にうれしいものなんでしょうか?

余因子行列の狙い/目的はなんでしょうか?(逆行列を求めるのに必要なものに名前を付けただけでしょうか?)

Chapter03_状態方程式
テイラー級数展開を用いたのは、なぜでしょうか?
テイラー級数展開を用いないと展開できないとかでしょうか?
式だけみても、テイラー級数展開を知っていなければ、難しいのかなと思いました。

出力方程式にy=Cx+Duとありましたが、これまでの講義でDという項はなかったのですがDはどういった意味をもっているのでしょうか。

線形化近似のところで、x_s=0でしたが、x_s=1のときはx~=x-1となり、状態方程式の展開時に定数項が出てくるかと思います。そのときはどう扱えばいいのでしょうか?

配列に対して、線形にプロットされるのは、線形近似を行っているからでしょうか?
出力を配列に切り替える意図がつかめませんでした。
これは,演習3.8のSimulinkモデルについてのご質問かと思いますが,To Workspaceの出力を配列にしているのは,MATLABの仕様上のテクニカルな理由によります.ただ,別の方法でグラフ表示するのであっても良いとは思います.
Chapter04_安定性
スライド番号59のモード展開の式変換が分かりません.
このようになれば負で安定というのは分かるのですが,なぜこうなるのでしょうか.
ここでのvの意味も教えて頂けると嬉しいです.


Chapter05_可制御性と可観測性
極零消去とは、本質的にはどういう状態のことでしょうか?
(具体的なイメージが付きにくいためご質問いたしました)

座標変換のT行列はどの様に決めるとよいのでしょうか?

Chapter06_状態フィードバック制御
応答特性を早くすると角周波数が暴れるイメージですか?
これは,望ましい極配置領域と過渡応答の関係に関するご質問かと思います.過渡応答は,図6.2の①の軸を左に移動させるとより速くなります.その際に,実軸に近い領域に配置しておけば,高い周波数成分が応答に現れることはありません.一方で,虚軸には近いものの,実軸から遠い部分に極が存在する場合,減衰は遅いものの,高い角周波数成分を持つ振動が生じます.これについては,演習6.1のプログラムで,極をpoles=[-0.01+50j,-0.01-50j]に設定すると確認できます.
なお,現実の機械システムで,応答を早くするために,フィードバック制御器のゲインを大きくし,閉ループ極を複素平面上の左に移動させると,しばしば激しい振動が生じます.これは,1)制御対象の位相が高周波帯域で想定外に遅れていたため閉ループ系が不安定化した,あるいは,2)入力飽和などの非線形性が存在したため閉ループ系が不安定化した,であることが多いと思います.今日では,これらの問題については,ロバスト制御を用いることで,システマティックに対処出来ます.
LQ最適制御について、評価関数を導入しそれが最小になるように設計できる手法と理解できました。
重みづけであるQ,Rは設計者が入力の大小や過渡応答の速さを決めていくという理解で合っていますでしょうか。
また、Mtlabの中で評価関数を最小化するフィードバックゲインを求める中でNという行列がありましたが、これは具体的に何を意味していますでしょうか。

LQ制御について質問です。
1.LQ制御を対象にした実際の設計は、設計者が重みQ,Rをトライ&エラーで変更して、自動的にFを決める方法と理解しましたが、あっていますでしょうか?
2.動画ではQを変更していていましたが、Qを触るケースとRを触るケースは、どのようなケースでしょうか。
このような場合ではQ、このような場合ではRという形だと分かりやすいです。
3.重みQを状態変数ごとに違う値を設定する、ということは安易にしていいものなのでしょうか?
重みを変更することの本質的な意味を知りたいです。
4.lqrコマンドの'N'は何を意味するのでしょうか。

聞き漏らしかもしれませんが、QとRはどのように調整したらよいのでしょうか?
P.89をご覧下さい.
Chapter07_サーボ制御
サーボ制御のスライドP,101の入力をどこに入れれば、同じような図形が出るかわからなかった。
ex71sim.slxについて,下図のように,3カ所を切断して頂き,①の部分にステップ信号を入力して頂ければと思います.
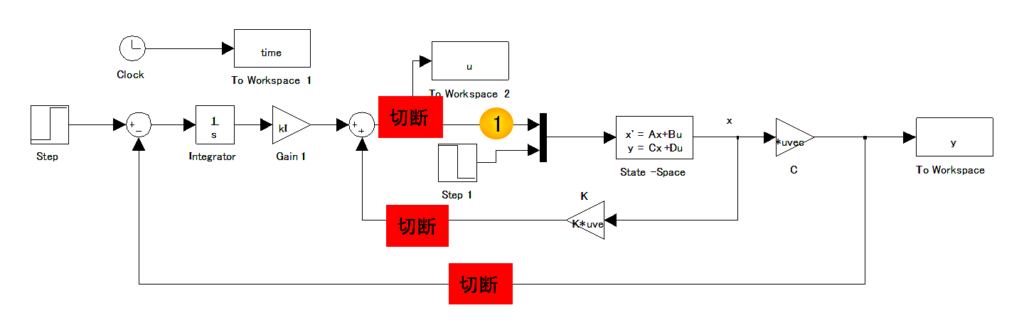
・p102でKclからKとKIを取り出しているのですが、具体的にどういう決め方でしょうか。要素番号の意味が分からないです。
・ステップ外乱dとありますが、ランダムノイズの場合でも適応可能でしょうか?

サーボ系における零点の影響を教えて頂きたいです。
第11章の二自由度制御の部分で,零点の影響についてご説明させて頂いております.
・零点は,安定零点(複素平面の左半平面の零点)であったとしても,虚軸に近いと過渡応答を悪化させる.逆に,
虚軸から十分に遠い場合には,過渡応答への影響は小さい.
・零点は,フィードバック制御により動かすことは出来ない.
その他,今回の講義では取り扱っておりませんが,不安定零点(複素平面上の右半平面の零点)は,逆応答を生じさせるので,非常に厄介です.ですが,物理的には致し方ない場合もあります.
Chapter08_出力フィードバック制御
xと^x(エックスハット)の必ずしも一致しない(遅れ時間等の関係)が安定性は担保される理由がまだ、自分なり解釈できない。
直感的な解釈は難しいところではありますが,フィードバック系の安定性については,P.121の結果(分離定理)より,保証されます.
一方で,制御系の過渡応答や外乱抑圧性能については,オブザーバによる推定誤差が制御性能の劣化につながります.その意味で,制御性能については,分離定理は成り立ちませんので,オブザーバの極の設定には注意が必要となります(第9章の演習課題).
積分型サーボ系でも同じようにオブザーバー(およびオブザーバーを用いた出力フィードバック制御)を設定することは可能なのでしょうか。
・可能です.これについては,第9, 10章の演習課題で取り扱っております.
・なお,P.132のようにオブザーバを用いた場合にも,閉ループ系の安定性は,分離定理より成り立ちます.
ex.81でA-LCを転置させてゲインLを算出しているのはなぜでしょうか?

出力フィードバック制御は任意に、A、Cが決定できる場合のみしか使用できませんか?
行列Aおよび行列Cは,制御対象の物理モデル,あるいは,使用できるセンサから決定されます.本講義で示しました出力フィードバック制御器は,「制御対象が可制御かつ可観測」である場合に設計可能です.
ただし,この条件は少しだけ緩めることが可能であり,演習2のCase3はその具体例になっております.実際,この課題では,制御対象は不可観測ですが,出力フィードバック系を構成出来ています.Case 3では,ヨーレートのみ制御し,不可観測な滑り角は成り行き任せで放っております.この例題の場合,滑り角のダイナミクスは安定なので,放っておいても特に問題は生じません.このように,直接制御できないけれども,安定なので放っておいても良い部分システムを含むシステムを「可安定」なシステムと言います.類似の概念に,「可検出」というものもあります.出力フィードバック系の設計は,「可制御・可観測」なシステムだけでなく,より緩いクラスである「可安定・可検出」なシステムに対して行うことが可能です.
実際に処理周期などの関係で挙動がずれている場合は,時間が経過すれば安定するというのは分かるのですが,
何らかの変化(外乱が変わる等)で不安定になることもないと思って大丈夫でしょうか.

Chapter09_演習1
・外乱をmuxブロックで入力しているのはなぜでしょうか。
外乱はuに足し算で入力するイメージが強いため、疑問に思いました。
(uに足し算で外乱を入れると式の意味あいが変わりますか?)
・今課題はSISOでしたが、MIMOでも同様の手法で解決できるのでしょうか。
・外乱は,入力に足し算に入る場合もありますが,一般にはそうではありません.この例題の場合には,外乱は負荷
軸に加わっております.このような場合,P.136のプログラムのように記述することで,数値シミュレーションを行
うことが可能です.なお,「uに足し算で外乱を加える」と,負荷軸ではなく,モータ軸に外乱が加わったことにな
ります.
・MIMOの場合にも,そのまま適用出来ます.
Chapter10_演習2
車両の状態方程式内にある、IZは何のパラメータでしょうか?

case2についてヨーレートは計測できているため、オブザーバーで予測する必要はないと思っています。
このケースでヨーレートはセンサ値を使い、すべり角のみをオブザーバーで予測する場合、どういう構成になるのでしょうか。
また、一部見えていてもすべてオブザーバーを使う方法と、一部のみオブザーバーを使う方法は、どちらの方法が優れているのでしょうか。
case3についてPIを用いてますが、このケースでも状態フィードバック制御は用いれますか?また、用いれる場合、PIと状態フィードバック制御のどちらが設計しやすいのでしょうか。Case1とcase3のブロック線図が似ている(係数比例の位置が違うだけ)ように思います。
本質的に同じなのでしょうか?サーボ系とPIについて解説をいただけると助かります。
Q) case2についてヨーレートは計測できているため、オブザーバーで予測する必要はないと思っています。このケースでヨーレートはセンサ値を使い、すべり角のみをオブザーバーで予測する場合、どういう構成になるのでしょうか。
A) 最小次元オブザーバを用いることにより,「一部の状態が直接観測可能である場合に,直接観測できない部分のみ推定する」ことが可能です.最小次元オブザーバについては,例えば,「吉川,井村: 現代制御論,昭晃堂(1994)」を参照頂ければと思います.
Q)一部見えていてもすべてオブザーバーを使う方法と、一部のみオブザーバーを使う方法は、どちらの方法が優れているのでしょうか。
A)オブザーバは「モデルを用いて推定する」手法でありますので,モデルの不確かさが大きい場合には,センサから直接得られる情報を用いた方が良いと思います.なお,ご質問とは少し異なる状況ですが,「位置の観測データが得られる場合に,それを微分して速度を算出する」こともあると思います.単純に微分を用いると,観測ノイズの影響が強く出ると思います.このような場合には,オブザーバを用いて速度を推定した方が良いかも知れません.
Q) case3についてPIを用いてますが、このケースでも状態フィードバック制御は用いれますか?また、用いれる場合、PIと状態フィードバック制御のどちらが設計しやすいのでしょうか。Case1とcase3のブロック線図が似ている(係数比例の位置が違うだけ)ように思います。
本質的に同じなのでしょうか?サーボ系とPIについて解説をいただけると助かります。
A)滑り角の値を直接取得出来る場合には,状態フィードバックを用いることが可能です.この場合,ヨーレートのみならず,滑り角の応答も制御出来ます.それに対し,PI制御の場合には,滑り角の応答は,ヨーレート制御の結果として,成り行きで決まるのみです.なお,Case3の場合には,観測情報としてヨーレートしか用いられておりません.それに対し,Case 1の場合には,ヨーレートと滑り角の両方を観測情報として用いております.この部分が,両者の本質的違いになっています.
何のために、PI制御を導入他のかいまいち不明だった。
また、PI制御による影響はどこに表れているのでしょうか。
Case3の場合,可観測ではありませんので,Case2と同様の手法により,出力フィードバック系を行うことは出来ません.そこで,適用可能な他の手法として.PI制御器を導入しました.この場合,Case2の形式の出力フィードバック制御器は設計出来ませんが,PI制御器でヨーレートのサーボ制御を行うことが可能であることを示しております.
Chapter11_二自由度制御
スライドp171 の式の2列目の()内の1/sはどこから出て来たのでしょうか.
11.5式からという説明がありましたが,一致してないように見えます.

(スライドp.176)
プラントへの外乱は,ステップ信号がよく用いられるのでしょうか?

フィードバック制御だけでは、オーバーシュート等を抑えられない、制御の組み合わせによって改善するしかないと理解しました。
オーバーシュートしてることがわかるならば、サチュレート又はフィルターしてしまえば、良いのかと直感的に思ってしまいますが、不都合等あるでしょうか?
※制御上で最適設計を行う上で知識の幅を増やしておきたいため、教えていただけると幸いです。
サチュレートとは,入力飽和のことかと思いますが,入力飽和は制御系の不安定化を招きますので,基本的に避ける方が良いと思います.ですが,Anti-windup補償の部分でご説明しましたように,制御対象や制御器のクラスによりますが,適切に設計したAnti-windup補償器を用いると,実用上それで十分な場合もあります.
一方で,フィルターとは,目標値フィルターのことかと思いますが,それも一種の二自由度制御です.ただし,目標値フィルターの場合には,目標値応答と外乱応答を完全には分離できません.そのため,不完全な二自由度制御ということになります.これに対し,本講義の二自由度制御の場合には,目標値応答と外乱応答が完全に分離しております.ただ,本講義で紹介しました二自由度制御は,「制御対象の完全なモデルが存在する」ことを前提としております.現実の制御問題は,そうではない場合も多く,その場合には,フィルタで目標値を鈍らせることで対処することになると思います.
p169の式11.5におけるGyrとGydの導出方法が分からないです。教えていただけますでしょうか。
p170にて、フィードバック系の特性方程式がGyrの分母=0になるのはなぜでしょうか。p170にて、11.8式でゲインの設定の選び方について、どういう選び方なのでしょうか。Gyrの式にはpが含まれており、pを変更すると零点が変わりそうな気がするのですが、変わっていない、ということなのでしょうか?零点についてあまり理解がなく。

例題ではPが伝達関数の例で示していますが、Pが状態空間表現で同じ式が記述されている場合でも成立する、でよろしいでしょうか?
また、MIMOの状態フィードバック制御器でも、二自由度制御系を組むことができるのでしょうか?
前提条件のプロパーな伝達関数とは、どういう状態の伝達関数のことでしょうか?
プロパーでない状態のとき、何が起きるのでしょうか?

Chapter12_入力飽和対策
2自由度の質問です。
名前の由来は、過渡応答と外乱抑制の2つがそれぞれ自由に設計できる、という意味で2自由度なのでしょうか?
目標値応答と外乱応答を独立に自由に設計出来る,ということから,二自由度制御と呼んでおります.
Chapter13_ロバスト制御概論
図13.1のブロック線図と,図13.4の左側のブロック線図は,同じ物として良いのでしょうか?

H∞最適制御問題のKが求まらないです。
算出の仕方がテキストにもないため、ご教示いただきたく。

ゲインスケジュールド制御についてです。
講義の中でも自動車が低速or高速では特性が変わってくる⇒その変化に合わせてコントローラーを設計できるとイメージできました。
演習がなかったため、実際に実装するとどうなるのか?が気になったのですが、おすすめの参考書があれば教えていただきたいです。
ゲインスケジュールド制御の理論的詳細については,例えば,
小原:行列不等式アプローチによる制御系設計,コロナ社,2016
をご覧頂ければと思います.また,応用例については,以下をご覧頂ければと思います.
小野,細江,浅野,菅,土居:ゲインスケジュールド制御による車両運動のロバスト安定化,計測自動制御学会論文集,Vol. 35, No. 3,
pp. 393-400, 1999
・ゲインスケジュールド制御は、一般的に車やロボットをプログラミングでコントローラ設計するとき、
if文で分岐して記述することは多々あるかと思いますが、そういうことでしょうか?
・式13.5のガンマは何を示す記号でしょうか。
・周波数応答のピーク値と誤差が式で比較されていますが、直感的につかめないです。
何かわかりやすく理解する方法はないでしょうか。

Chapter14_モデル予測制御概論
Chapter14_モデル予測制御概論に関するご質問・モデル予測制御問題のコスト関数最小化として,どのような手法が用いられることが多いでしょうか?
モデル予測制御の場合、実装する上では計算量と安定性が問題になりそうだと感じました。
操作量を更新するサンプリング周期よりも短い時間で最適制御の計算が終わらなければ、フィードバック制御は実現できないかと思われます。通常、最適制御問題(特に非線形)は解の修正を繰り返して最適解に収束させるため、機械系などのミリ単位のサンプリングが要求されるモデルにはどのように使用するのでしょうか。
モデル予測制御では,計算量と安定性が問題になるのはご指摘の通りです.まず,安定性につきましては,資料P.229のコスト関数の最後の項(終端重みと言います)の行列Pを適切に設計することで保証されることが知られています.その他,モデル予測制御の場合には,「制約付き最適化問題をサンプル時刻毎に解く」ことになりますが,「制御実行中に制約を満たす解が存在しなくなる」ことを避ける必要もあります.これについては,P.229の最適化問題に,終端制約を加えることで実現出来ることが知られています.ただ,こうした理論的保証を厳密に行おうとすると,オフラインでの制御器設計やオンラインで最適化問題を解くことが難しくなる傾向があります.
モデル予測制御の制約付き最適化問題は,一般に,ニュートン法等の勾配計算に基づく手法で計算されます.制御対象の非線形性が強くない場合には,制御対象のモデルを線形時不変系としておけば,最適化問題は凸二次計画問題(QP)となります.QPについては,高速なソルバーが存在し,それなりに規模の大きい問題でも,ミリ秒で解くことが可能です.個人的には,このクラスの制御手法(およびその多少の拡張)で扱える問題の範囲は広いと考えております.一方で,制御対象の非線形が強い場合には,非線形モデル予測制御を使った方が良い結果を与える場合もあると思われます.この場合,非線形最適化問題をサンプル時刻毎に解くことが必要になります.これについては,世界中で様々なタイプのソルバー(例えば,qpOASES,FORCESPRO,CGMRES)の開発が続けられています.

