MBD現代制御システム設計研修‐基礎・実践編‐
目次
Part1 MATLAB/Simulinkによるモデル構築
MBDプロセス研修のページをご参照ください。
Part2 状態空間表現とシステムの自由応答
演習を通じて、微分方程式と状態空間表現で差がないことが確認でき理解が深まりました。
1入力1出力のシステムに限って言えば、どちらで表現するのが良いなどメリット・デメリットはあるのでしょうか。
おっしゃるように状態空間表現は微分方程式で導出された式を状態空間表現という統一的な表現に整理しているにすぎません。形式が統一された状態空間表現を用いることで,後ほど説明する極配置制御系やオブザーバーなどがシステムによらず同じ手順で実現することができるようになります。
デメリットとしては,慣れないうちは状態変数の定義をどのようにするかを悩むケースが多いですが,物理現象がはっきりしている場合は,スライド2-26のような考え方で設定をすると比較的簡単に状態変数を設定することができるかと思います。
MBDでは、mスクリプトを使用して実行していますが、Simlinkで配列を実装するためには、どのような知識が必要でしょうか?具体的には、①入力一つ出力一つ。②配列1を出力とする③配列1と違う値が入力された際は、配列2にその値を入れる④配列は基本的に、500ms後に1段上がる⑤配列2に99(空の値)が入っている場合は、一段上げずにkeepする⑥一段上がった後に最後の配列に空の値(99)を入れる
時刻に依存した信号波形を作成されたい場合は,SourcesブロックにあるSignal Builderブロックを用いるとよろしいかと思います。また,単純なステップ状の波形の場合は,事前にMATLABで配列を作成しFrom Workspaceを用いて取り出すという方法もございます。
微分方程式を立てたとき、左辺がx_d(t)となり、Simulinkモデルで微分方程式を表現するとき、出力ポートがx(t)となるのはなぜでしょうか。
まず,微分方程式に基づくモデリングにおいてほしい情報はxの時間変化x(t)です。x_dは,システム出力(この場合x)の時間変化に関する情報を示しています。各時刻におけるx_dを積み重ねる(積分する)ことで出力xを取り出せることから,モデリングで最も重要なことは出力に関する微分方程式x_dを導出することであり,これが「モデリング=微分方程式の導出」ということになります。
状態空間表現は有限要素法等に近い考えなのでしょうか?
そのようにとらえていただいて結構かと思いますが,詳細については後半担当講師の和田先生にお問い合わせをいただけますと幸いです。
λ=0という結果が出ましたが、その場合は安定の領域に入りますか?それとも不安定になりますでしょうか?
固有値の実部が0となる極(固有値)ではシステムが安定限界となります。
極を1つだけもつシステム場合,システムの応答は以下のような応答となり,持続振動や0に収束しないなどの挙動を示します。
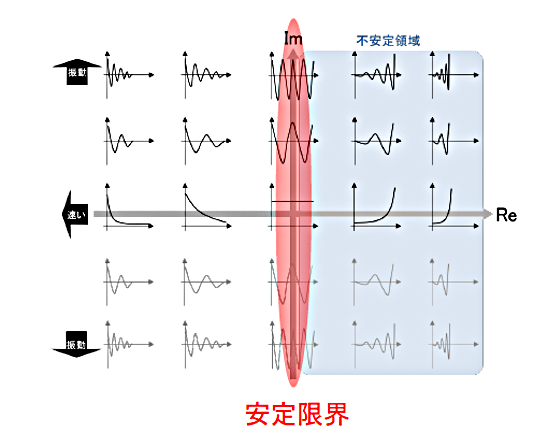
自由システムの理解がいまいぼんやりしています.
システムの安定性を見たいときに使うといった理解でよろしいでしょうか?
はい,そのご理解で結構です。システム自身がどのような初期値を持っていても入力u=0の条件下において,状態変数が発散せずに0へ収束する(すなわち安定)という性質ですので,システム固有の安定性を評価していることになります。
行列の固有値と固有ベクトルは、3次元だとどのようなイメージになるのでしょうか。
(講義内で2次元平面でないと表現できないとありましたのが、可能であればお願いします)
説明がわかりにくく申し訳ございません,3次元の場合も3次元空間上で同様の定義となります(4次元以上は図示することが困難です)。
考え方はなんとなく理解したが、自分なりの解釈に落とし込めない。線形代数の基礎を勉強し直せば理解がしやすくなるのでしょうか?
特に数学的にややこしく感じる点は,システムの自由応答かと思います。Part3で自由応答に基づく制御系およびオブザーバの設計論に展開することで,学んできたことの意味が分かるかと思いますので,とりあえずはPart3へお進みいただく方がよろしいかと思います。
(線形代数は基本的には,演算のルールについて理解をいただいていれば問題ないかと思います。)
微分積分の基礎があれば理解がしやすいのですか?
微積の問題を解く力よりも,微分・積分を用いたモデリングの基本的な考え方を理解いただくことが重要かと思います。
ぜひとも,Part2_01_補足01_微積の復習(講義:約21分)(MBDプロセス研修)~Part2_01_補足05_モデリングのための基本法則(講義:約16分)(MBDプロセス研修)の考え方を復習いただき理解の手助けとしていただければと思います。
Part3 状態フィードバック制御系の設計
Luenbergerオブザーバーはプロトタイプのものと比較し、推定性能が良いと確認できました。
オブザーバーゲインをどうするのかというところもポイントなのかと理解しましたが、これも最適に設定することが望ましいのでしょうか。
安定化制御において、どんな初期値においても、状態量を0に制御するのは、とても興味深い内容だと思う。
安定化までの時間がかかってしまうと、物理現象的には、倒れてしまう等の事が発生してしまうのではないかと思うが、安定化までの時間については、PIDで制御する?法が望ましいのでしょうか?
安定化までの応答速度は極の位置(特に実数部を大きな負の値に取る)ことによってコントロールすることができます。Part 3で説明しますが,状態フィードバックでは複数の状態変数を同時に制御したい場合にその効果を発揮します(PID制御は原則として1変数しか制御できないため)。そのため,システムが一入力一出力系の場合はPID制御法を適用することを検討してもよろしいかと思います(他者が見ても構造がわかりやすいため)。
可制御性・可観測性の判別式について、
式の計算を進めると3-29のような形になるので、可制御性・可観測性を調べることができる、ということなのでしょうか?
また、実際に設計を進めるうえで可制御性・可観測性を調べる場合は、判別式を使うことが通常の方法でしょうか?
はい,状態変数変換によって内部の構造を変換(見やすく)することで可制御・可観測性を調べることができるということになります。
一般的には,判別式を用いるケースの方が多いかと思います。
併合システムの設計(3-33)について、オブザーバーの状態変数x_hat(t)を状態フィードバック制御器に入力しているように読み取れます。
実際の設計では、一部の状態変数はセンサで正確に読み取り(x(t))、見えない状態変数はオブザーバーで推定する(x_hat(t))、といったことが考えられますが、センサで取得した状態変数とオブザーバーで推定した状態変数を混ぜて使う場合、どのようなブロック線図になるのでしょうか?
そもそも、すべてオブザーバーで推定した状態変数を状態フィードバック制御器にいれることが正しいことであり、混ぜて使うというのは間違った方法なのでしょうか?また、混ぜた時も分離定理は成り立つのでしょうか?
センサで観測できるシステムにおいてオブザーバを用いる場合には,観測できない変数のみを推定する最小次元オブザーバを用います。
これにより,測定値と推定値を併用することが可能です。
オブザーバーによる状態推定を初めてしった。
イメージとしてプログラム等に使用されることが多いのでしょうか?
オブザーバはいわゆるソフトセンサの一種ですので,組み込み制御器などでプログラムとして実装されます。
パート3の内容は、サーボ問題にも適応できる問題なのでしょうか?
サーボ問題の場合、別の切り口で設計していくものなのでしょうか?(車の設計では、サーボ問題を扱うことが多いため)
今回取り扱った1入力1出力系(内部状態はn次元)の場合は,外側に積分制御(いわゆるI制御)を加えることで,サーボ系が構成されます。そのため,状態フィードバック制御器で安定化および応答性能の変更を行い,(一定値)外乱の除去ならびに追従性を積分動作にて補償する構成が考えられます。基本的な設計法については,下記参考書籍などをご参照ください。
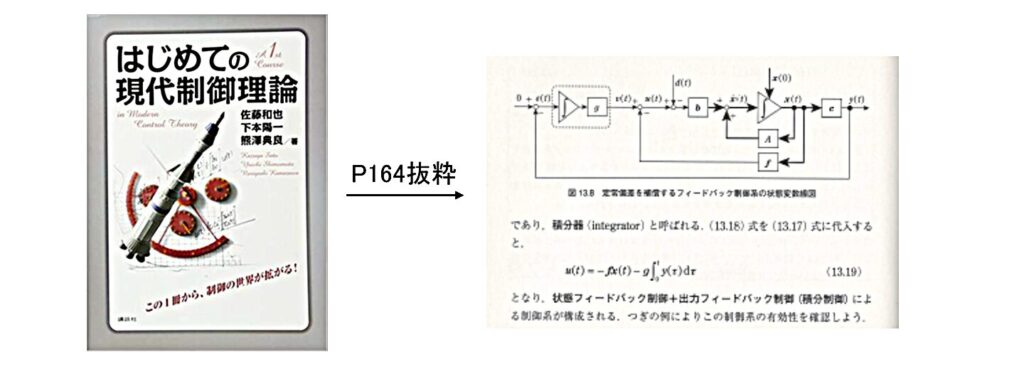
次の講義で出てくるかもしれませんが、併合システムはどのようなシステムを設計するのに優れている等あるでしょうか?
併合システムは「状態フィードバック制御+オブザーバ」によって構成されるシステムです。本来ならば状態フィードバック制御器を構築する際には,すべての状態変数がセンサ等で取得できることが望ましいのですが,それができない場合において,オブザーバを併用することで制御系設計を可能としております。言い換えれば,状態量をすべて直接的にセンシングできなくても制御系が構築できるという点が優れているといえます。
制御には精通していないため、カルマンフィルタの名前だけは聞いたことあるんですが、どのような役割で、何をしている等は分からないため、ご教示いただくことは可能でしょうか。
カルマンフィルタは,オブザーバゲインを自動的に決定するアルゴリズムの一種になります。そのため,本研修の関連からオブザーバの一種という見方ができます。
演習問題1について、解答がなく、FBゲインの導出が違うのか、オブザーバゲインの導出が違うのか、FBゲインの極設定やオブザーバゲインの極設定が違うのか、はたまたモデルが違うのか、またどうなったら正解なのかがわかりません。
LMS(etudes)内の
ホーム > カテゴリ >現代制御システム設計研修
> 基礎・実践編
> 09_演習課題解答
> 現代制御_Part3_演習課題解答
に課題解答を掲載しておりますのでご確認ください。
自由システムについての理解を深める為、インターネットで検索してみたのですが、あまり見つかりませんでした。
別の呼び方などがあるのでしょうか?
自由システムの応答そのものを指し「システムの自由応答」と表記する場合もございます。
実際にシステムとして可制御性、可観測性を知るために状態変換行列を出そうとしたときには、システムの状態方程式と固有値から算出するのでしょうか?
システム行列Aの固有ベクトルを求めこれらを順に並べることにより状態変換行列が生成されます。

Part4 実践!クレーンシステムの状態フィードバック制御
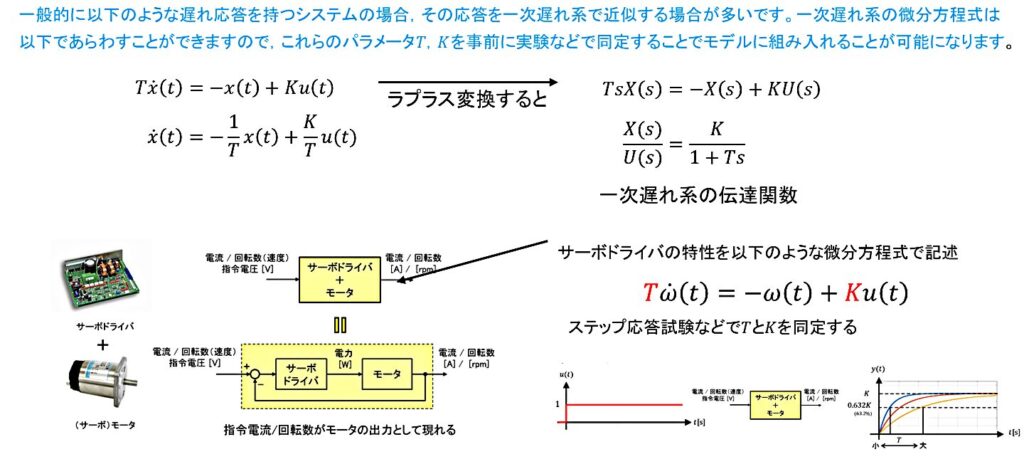
サーボドライバとその対象(テキストではモーター)が無視できないダイナミクスを持つ場合、どのように式を設定すればよいのでしょうか。
また、ダイナミクスの遅れ(時間等)がおおむね既知の場合、どのように式を設定すればよいのでしょうか。
また、サーボドライバの出力が観測できず(テキストでは電力)、指令電圧と出力電流しか観測できない場合において、さらにダイナミクスが無視できないとき、どのようなアプローチで進めるのがよろしいでしょうか。
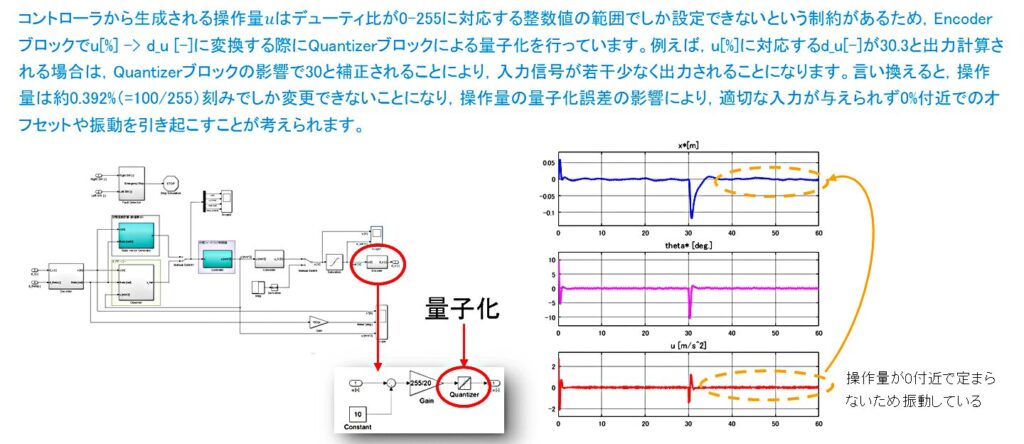
quantizerを使用することで、誤差が大きくなってしまう事は理解できたのですが、
quantizerブロックを使うメリットとしては、線形値から、離散信号に変換し、計算のタイミングをそろえたいという事でしょうか?
量子化ブロックのメリットがいまいちピンときていません。
QuantizerはA/D変換器の量子化特性を表したものです。そのため,Quantizerブロックを積極的に挿入することによるメリットはほぼありません。しかしながら,アナログ信号値をコンピュータが変換可能なデジタル信号値に変換するにはA/D変換器が必須になるため結果的に,Quantizerブロックによる量子化誤差をモデル上で考慮せざるを得なくなります。
数式を追っていたため、少しイメージがつきにくかったのですが、クレーンモデルをシミュレーションしてみることでこれまでの流れを理解することができました。
1.実機のコントローラーとHILシミュレーターがボード形式なので毎回混乱してしまうのですが、
最後のHILS演習はコントローラー(実機)+クレーン(仮想)の理解であってますでしょうか。
2.脇谷先生がラップアップの場で説明していたものは上記のクレーンが実機に置き換わったと理解していますが、
この時PC(Matlab)も繋がっていると思いますが、PCは何の役割をしているのでしょうか。シミュレーションの実行と結果のモニタリングでしょうか。
勝手なイメージですが、全部実機に置き換わればクレーンを動かして狙いの動きとなるように制御が働くのではと思いました。Matlabと実機の関係性で混乱しております。
3.最後の動画で台車は制御によって0の位置で制御できることを確認できましたが、0の位置ではなくユーザーの決めた位置で制御することは可能なのでしょうか。
1.はい,ご認識の構成で間違いありません。
2.はい,PCはモデルの書き込みと実機結果のモデルのモニタリングのみに使用しています。実際の制御中には,Controllerボードに書き込まれたアルゴリズムが制御を行っています。そのため,モニタリングを行わなければPCは不要で,コントローラボード単体での制御も可能です(この場合,モデルをエクスターナルモードではなくスタンドアローンモードで書き込む必要があります)。
3.位置だけをずらす場合には,例えば,入力されるセンサ出力から定数を引くことで台車の位置を意図的にずらすことができます。

HILS演習のオブザーバーゲインとフィードバックゲインの極について教えてください。
テキストおよび動画で指定していただいた極の値ではほぼ0近傍に推移していることを確認できましたが、
ゲインを変えた際にどのようなふるまいをするか確認していたところ、0の位置から少しずれた(オフセットした)位置で推移しました。
これは単純にゲインの設定方法がまずいということでしょうか。(この時の設定値:オブザーバーゲインテキストのまま(-5,-10-2,-4)、フィードバックゲイン:(-2,-8,-4,-7))